Initializing neural networks
www.deeplearning.ai](https://www.deeplearning.ai/ai-notes/initialization/index.html#I)
의 내용을 최대한 번역한 내용이다.
I The importance of effective initialization
머신러닝 알고리즘을 설계하기 위해서는, 모델의 아키텍쳐(Logistic regression, Support Vector Machine, Neural Network 등) 를 정의한 후에 파라미터를 학습하도록 훈련시킨다.
- 파라미터들 초기화시킨다.
- optimization algorithm(Adam, Momentum, Batch Gradient Descent 등)을 선택한다
- 다음 과정을 반복한다.:
- input을 propagate 한다.
- cost function을 계산한다.
- backpropagation을 사용하여 파라미터들에 관하여 cost의 gradient를 계산한다.
- optimization algorithm에 따라, gradient를 이용하여 각 파라미터들을 업데이트 시킨다.
그 후 새로운 data point가 주어지면, data의 class를 예측하기 위해 모델을 사용할 수 있다.
initialization 단계는 모델의 최종적인 성능에 중요하며, 정확한 방법이 필요하다. 이를 설명하기 위해 아래의 3 layer neural network를 살펴보길 바란다. 여러 방법으로 네트워크를 initialization하고 학습에 미치는 영향을 관찰할 수 있다. (위의 페이지에서 직접 해보는 것을 권장)
initialization 방법이 Zero일 때 gradient와 weight에 대해 무엇을 알 수 있을까?
모든 weight를 0으로 초기화하면 뉴런이 훈련 중에 동일한 feature을 학습하게 된다.
사실, 어떤 constant initialization 방법을 사용하여도 성능이 매우 좋지 않다. 두 개의 hidden unint이 있는 신경망을 고려하고 모든 bias을 0으로 초기화하고 weight를 상수 $\alpha$로 초기화한다고 가정해보자. 만약 input ($x_{1}, x_{2}$)가 전파되는 경우, 두 hidden unit의 output 모두 $relu(\alpha x_{1} + \alpha x_{2})$가 될 것이다. 따라서, 두 hidden unit은 cost에 동일한 영향을 미치므로 동일한 기울기로 이어진다. 따라서 두 뉴런은 훈련 전반에 걸쳐 symmetric f이게 되고, 서로 다른 뉴런이 서로 다른 것을 학습하지 못하게 된다.
가중치 값을 너무 크거나 작게 설정하면 cost의 plot에 관하여 무엇을 알 수 있나?
symmetry가 없어졌음에도 불구하고, 가중치를 (i) 너무 작게 혹은 (ii) 너무 크게 설정하면 각각 (i) 학습이 느리거나 (ii) 발산하게 된다.
효율적인 학습을 위해서는 적절한 초기화 값을 선택하는 것이 필요하다. 다음 섹션에서 이에 대해 자세히 살펴본다.
II The problem of exploding or vanishing gradients
9-layer neural network를 생각해보자.

optimization loop (forward, cost, backward, update)의 매 iteration에서 output layer에서 input layer로 이동할 때 backpropagate된 gradient가 증폭되거나 최소화되는 것을 볼 수 있다. 다음 예를 보자.
모든 activation function이 linear (identity function)이라고 가정하자. 그러면 output activation은
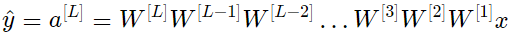
L = 10이고 W는 layer [1] 에서 [L - 1] 이 모두 2 neuron이고 2 input을 받기 때문에 모두 (2,2)의 matrix이다. 이를 염두에 두고 설명을 위해 모든 layer의 W를 W이라고 가정하면, output의 prediction은 $\hat{y} = W^{[L]}W^{L-1}x$ 이 된다.
너무 작은 초기값 또는 너무 큰 초기값, 적절한 초기화 값의 결과는 무엇입니까?
Case 1: A too-large initialization leads to exploding gradients
모든 가중치가 identity matrix보다 약간 크게 initialized 되는 경우를 고려해보자.
이것은 $\hat{y} = W^{[L]} 1.5^{[L-1]} x$ 로 단순화할 수 있고 $a^{[l]}$의 값은 $l$에 대해 exponential하게 증가한다. 이러한 활성화가 backward propagation에 사용되면 exploding gradient 문제가 발생한다. 즉, parameter에 대한 cost의 gradient가 너무 크다. 이로 인해 cost가 minimum value 주위에서 진동하게 된다.
Case 2: A too-small initialization leads to vanishing gradients
마찬가지로, 모든 가중치가 identity matrix보다 약간 작게 initialized되는 경우를 고려해보자.
이것은 $\hat{y} = W^{[L]} 0.5^{[L-1]} x$ 로 단순화할 수 있고 $a^{[l]}$의 값은 $l$에 대해 exponential하게 감소한다. 이러한 활성화가 backward propagation에 사용되면 vanishing gradient 문제가 발생한다. 즉, parameter에 대한 cost의 gradient가 너무 작다. 이로 인해 cost가 minimum value에 도달하기 전에 수렴된다.
대체로 적절하지 않은 값으로 가중치를 초기화하면 신경망의 학습이 divergence 되거나 매우 느려진다. 간단한 symmetric weight matrix로 exploding / vanishing gradient 문제를 살펴보았지만, 이러한 관찰 결과는 너무 작거나 너무 큰 초기값을 사용했을 때도 일반화 될수 있다.
III How to find appropriate initialization values
네트워크의 gradient가 사라지거나 폭발하는 것을 막기 위해 다음과 같은 법칙을 고수할 것이다.
- The mean of the activations should be zero.
- The variance of the activations should stay the same across every layer.
이러한 두가지 가정하에, backpropagated gradient signal은 어느 layer에서도 너무 작거나 너무 큰 값으로 곱해지면 안된다. 폭발하거나 사라지지 않고 input layer로 이동해야한다.
보다 구체적으로 레이어 $l$을 고려해보자. forward propagation는 다음과 같다.

우리는 다음을 유지하려고 한다.

zero-mean을 보장하고 모든 layer의 입력 분산 값을 유지하면 잠시 후에 설명할 폭발/소실 신호가 없음을 보장한다. 이 방법은 forward propagation (for activations) 와 backward propagation (for gradients of the cost with respect to activations)에 모두 적용된다. 권장하는 초기화는 모든 layer $l$에 대해 Xavier 초기화(또는 파생된 방법 중 하나)이다. 즉, layer $l$의 모든 가중치는 normal distribution에서 무작위로 선택된다.
아래의 시각화는 5-layer fully-connected neural network에 대한 각 layer의 활성화에 대한 Xavier 초기화의 영향을 보여준다. (위의 페이지에서 직접 해보는 것을 권장)
Glorot et al. (2010)에서 이 시각화 결과 이면의 이론을 찾을 수 있다. 다음 섹션에서는 Xavier initialization에 대한 mathematical justification을 제시하고 효과적인 initialization인 이유를 보다 정확하게 설명한다.
IV Justification for Xavier initialization
이 세션에서, Xavier initialization은 모든 layer에서 동일한 variance를 유지한다는 것을 보여줄 것이다. layer의 activations가 일반적으로 0 근처에 분포한다고 가정한다. 보통은 개념을 파악하기 위해 mathematical justification 을 이해하는 것이 도움이 되지만 수학 없이도 근본적인 아이디어를 이해할 수 있다.
(III) 파트에서 설명된 layer l 에서 설명을 진행하고 activation function이 tanh라고 가정하겠다. forward propagation은 다음과 같다.
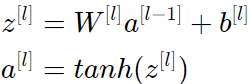
l-1 layer의 분산과 l layer의 분산 사이의 관계를 도출하는 것이 목적이다. 그 후에 우리는 그 둘의 분산을 어떻게 같게 할지 이해하게 될 것이다.
네트워크를 적절한 값으로 초기화하고 input을 normalize한다고 가정하자. 훈련 초기에 네트워크는 tanh의 linear regime에 있다. value는 충분히 작으므로 tanh(z[l])≈z[l]이며, 즉 다음을 의미한다.
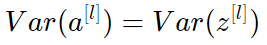
또한, $ z^{[l]}$ = $W^{[l]}a^{[l−1]}$ + $b^{[l]}$ = $vector$($z_{1}^{[l]}$, $z_{2}^{[l]}$, ..., $z_{n}^{[l]}$)
따라서 이전 방정식에서 요소별로 살펴보면

일반적인 math trick은 variance 바깥의 합을 계산하는 것이다. 이를 위해서는 다음 세 가지 가정을 해야 한다.
- Weight는 독립적이고 동일하게 분포됩니다.
- Input은 독립적이고 동일하게 분포됩니다.
- Weight와 input 은 상호 독립적이다.
따라서, 다음과 같은 식을 얻을 수 있다.

또 다른 일반적인 트릭은 곱의 분산을 분산의 곱으로 변환하는 것이다. 공식은 다음과 같다.


거의 끝났다! 가중치의 평균이 0으로 초기화되고 input도 normalized 되기 때문에 첫번째 가정과 두번째 가정에 따라 $w$의 평균이 0이고 $a$의 평균도 0이다. 따라서:
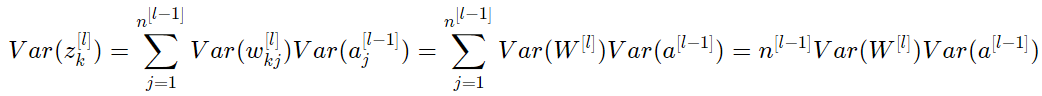
위의 equality 은 다음과 같은 첫 번째 가정으로부터 온다.

마찬가지로 두번째 가정으로부터
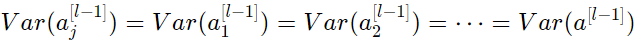
동일한 아이디어로
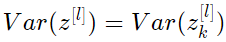
모든 것을 요약하면 다음과 같다.
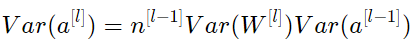
놀랍게도, variance를 전 layer에 걸쳐서 같도록($Var(a^{[l]}) = Var(a^{[l-1]})$ 유지하려면, $Var(W^{[l]})$ = $ \frac{1}{n^{[l-1]}} $ 일 필요가 있다. 이는 Xavier initialization를 사용한 variance 선택을 정당화한다.
이전 단계에서는 특정 layer $l$을 선택하지 않았다. 따라서 우리는 이 표현이 네트워크의 모든 layer에 적용됨을 보여주었다. $L$을 네트워크의 output layer라고 하자. 모든 layer에서 이 표현식을 사용하여 output layer의 variance을 input layer의 variance에 연결할 수 있다.
가중치를 초기화하는 방법에 따라 output과 input의 분산 관계가 크게 달라진다. 다음 세 가지 경우를 살펴보자.
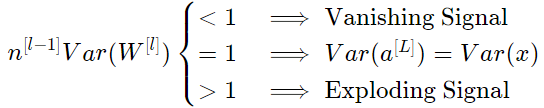
따라서 forward propagated signal의 vanishing 또는 exploding을 방지하려면 $Var(W^{[l]}) = \frac{1}{n^{[l-1]}}$ 으로 초기화함으로써 $n^{[l-1]} Var(W^{[l]}) = 1 $으로 설정해야한다.
Conclusion
실제로 Xavier 초기화를 사용하는 기계 학습 엔지니어는 가중치를 $N(0, \frac{1}{n^{[l-1]}})$ 또는 $N(0, \frac{2}{n^{[l-1]} + n^{[l]}})$로 초기화한다. 후자 distribution의 분산 항은 $\frac{1}{n^{[l-1]}}$와 $\frac{1}{n^{[l]}}$의 조화 평균이다.
이것이 Xavier initialization의 theoretical justification이다. Xavier initialization은 tanh activation와 함께 작동한다. 무수한 다른 초기화 방법이 있다. 예를 들어 ReLU를 사용하는 경우 일반적인 초기화는 He 초기화(He et al., Delving Deep into Rectifiers)이며 여기서 가중치는 Xavier initialization의 분산에 2를 곱하여 초기화된다. 이 초기화에 대한 justification는 약간 더 복잡하지만 tanh에 대한 것과 동일한 과정을 따른다.