인공지능을 위한 선형대수(전사함수와 일대일함수)
edwith에서 들을 수 있는 인공지능을 위한 선형대수(주재걸 교수님) 강의를 들으면서 복습한 내용입니다.

- ONTO: 공역 = 치역 (치역은 공역의 부분집합), 전사라고도 함
- 정의역의 개수가 공역보다 더 많을 때 ONTO일 가능성이 커짐
- 공역에 mapping되는 정의역의 원소가 최소 하나는 존재해야한다.
- 학습된 선형변환에 의해서 출력되는 결과가 치역, 640x480x3이 공역이 될 수 있음 (가능한 모든 픽셀 조합)
- 실제 데이터가 존재할 법한 구불구불한 평면(치역, sub 공간)을 manifold라고 부름

- 3차원에서 2차원으로 갈 때는 one-to-one이 될 수 없음
- 3차원 공간에 vector가 4개 주어져 있을 때 무조건 linearly dependent한 것을 알 수 있다.

- NN이 유의미한 feature를 추출할 수 있음

- 과체중을 만들어 내는 사람이 여러 명 있더라도 1개의 값으로 mapping이 된다. 세세한 차이들이 다 존재하는 경우로 입력을 구성하더라도 수명을 예측하기 위해서 유용한 정보만 남기고 의도적으로 입력값에서의 자잘한 차이를 없애준다.
- 정보를 손실하는 과정이라고도 볼 수 있음
- 의도적으로 불필요한 정보를 0으로 만들어준다고 생각하면 됨
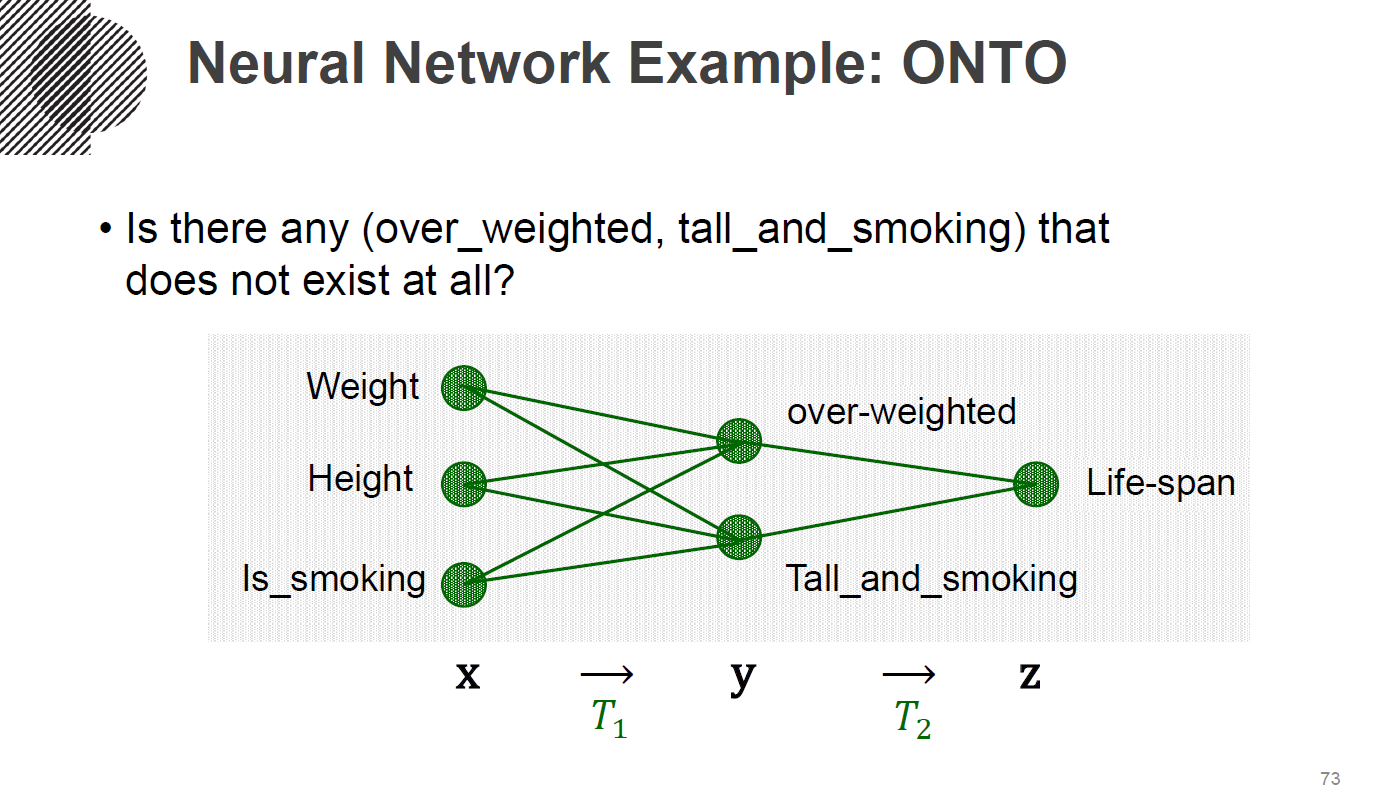
- 입력 vector를 다양하게 구성하더라도 출력 vector의 공역을 다 cover할 수 있나?
- 항상 onto(전사) 하느냐? 모름
- 다양한 조합 중 학습한 mapping은 2차원의 모든 부분에 mapping이 되도록 학습하는 것이아니라 일부분으로 mapping 되도록 학습될 수 있음
- 필요한 부분으로의 mapping을 배우는 것이지 전사의 mapping을 학습하는 것이 아님

- T 함수가 one-to-one이라는 뜻은 A의 column vector들이 linearly independent 하다는 의미
